$\,1.\,$ Draw the graph of the function $\,\,y=\frac{x^2}{x}\,\,$ and from the graph evaluate $\,\lim_{x \to 0}\frac{x^2}{x}.$
Sol. From the graph, using the definition of limit, we can evaluate the limit of the given function i.e., $\,f(x)=\frac{x^2}{x}.$
Let us denote Left hand limit by L.H.L. and Right hand limit by R.H.L.
Then, L.H.L.$=\lim_{h \to 0} f(0-h)\\=\lim_{h \to 0}\frac{(0-h)^2}{(0-h)}\\=\lim_{h \to 0}\frac{h^2}{-h}\\=\lim_{h \to 0} (-h)\\=0.$
Similarly, R.H.L.$=\lim_{h \to 0}f(0+h)\\=\lim_{h \to 0}\frac{(0+h)^2}{(0+h)}\\=\lim_{h \to 0}\frac{h^2}{h}\\=\lim_{h \to 0} (h)\\=0$
$\,\therefore \,$ L.H.L.=R.H.L. .So, the limit exists and its value is $\,0.$
$\,2.\,$ Sketch the graph of $f(x)=1, \,\text{for}\,\, x >0\\f(x)= x^2, \text{for}~~ x \leq0$
Sol. Hints : Follow S N De work out problem: [EXAMPLE $\,\,7$]
Prove :
$\,3(i)~~ \lim_{x\to 4} \frac{3-\sqrt{5+x}}{1-\sqrt{5-x}}=-\frac 13$
Sol. $~~ \lim_{x\to 4} \frac{3-\sqrt{5+x}}{1-\sqrt{5-x}}\\=\lim_{x \to 4}\frac{(3-\sqrt{5+x})(1+\sqrt{5-x})}{(1-\sqrt{5-x})(1+\sqrt{5-x})}\\=\lim_{x \to 4} \frac{(3-\sqrt{5+x})(3+\sqrt{5+x})(1+\sqrt{5-x})}{[1^2-(\sqrt{5-x})^2](3+\sqrt{5+x})}\\=\lim_{x\to 4} \frac{(3^2-5-x)(1+\sqrt{5-x})}{(1-5+x)(3+\sqrt{5+x})}\\=\lim_{x\to 4}\frac{-(x-4)(1+\sqrt{5-x})}{(x-4)(3+\sqrt{5+x})}\\=-\frac{1+\sqrt{5-4}}{3+\sqrt{5+4}}\\=-\frac{1+\sqrt{1}}{3+\sqrt{9}}\\=-\frac{1+1}{3+3}\\=-\frac 26\\=-\frac 13\,\,\text{(proved.)}$
$3(ii)~~\lim_{x \to 1}\frac{x^2-\sqrt x}{\sqrt x-1}=3$
$\,\text{Sol.}~~\lim_{x \to 1}\frac{x^2-\sqrt x}{\sqrt x-1}\\=\lim_{x \to 1} \frac{(x^2-\sqrt x)(\sqrt x+1)(x^2+\sqrt x)}{(\sqrt x-1)(\sqrt x+1)(x^2+\sqrt x)}\\=\lim_{x \to 1}\frac{[(x^2)^2-(\sqrt x)^2](\sqrt x+1)}{[(\sqrt x)^2-(1)^2](x^2+\sqrt x)}\\=\lim_{x \to 1}\frac{(x^4-x)(\sqrt x+1)}{(x-1)(x^2+\sqrt x)}\\=\lim_{x \to 1} \frac{x(x^3-1)(\sqrt x+1)}{(x-1)(x^2+\sqrt x)}\\=\lim_{x \to 1}\frac{x(x-1)(x^2+x+1)(\sqrt x+1)}{(x-1)(x^2+\sqrt x)}\\=\lim_{x \to 1}\frac{x(x^2+x+1)(\sqrt x+1)}{x^2+\sqrt x}\\=\frac{1(1^2+1+1)(\sqrt 1 +1)}{1^2+\sqrt 1}\\=\frac{3 \times 2}{2}\\=3\,\,\text{(proved)}$
$\,3(iii)~~~\lim_{x \to 0} \frac{1-\cos x \sqrt{\cos 2x}}{x^2}=\frac 32.$
Sol. $~~~\lim_{x \to 0} \frac{1-\cos x \sqrt{\cos 2x}}{x^2}\\=\lim_{x \to 0} \frac{(1-\cos x \sqrt{\cos 2x)}(1+\cos x\sqrt{\cos 2x})}{x^2 (1+\cos x\sqrt{\cos 2x})}\\=\lim_{x \to 0}\frac{[1-\cos^2x(\cos 2x)]}{x^2(1+\cos x\sqrt{\cos 2x})}\\=\lim_{x \to 0}\frac{1-(1-\sin^2x)\cos 2x}{x^2(1+\cos x\sqrt{\cos 2x})}\\=\lim_{x \to 0}\frac{1-\cos 2x+\sin^2x\cos 2x}{x^2(1+\cos x\sqrt{\cos 2x})}\\=\lim_{x \to 0}\frac{2\sin^2x+\sin^2x\cos 2x}{x^2(1+\cos x\sqrt{\cos 2x})}\\=\lim_{x \to 0}\frac{\sin^2x(2+\cos 2x)}{x^2(1+\cos x\sqrt{\cos 2x})}\\=\lim_{x \to 0} \frac{\sin^2x}{x^2} \cdot \lim_{x \to 0}\frac{2+\cos 2x}{(1+\cos x\sqrt{\cos 2x})}\\=1 \cdot \frac{2+1}{1+1 \cdot 1}\\=\frac 32\,\,\,\text{(proved)}$
$\,4.\,$ Prove
$\,(i)\,\, \lim_{n \to \infty} (\sqrt{n+1}-\sqrt{n})=0$
Sol. $\,\lim_{n \to \infty} (\sqrt{n+1}-\sqrt{n})\\=\lim_{n \to \infty}\frac{(\sqrt{n+1}-\sqrt{n})(\sqrt{n+1}+\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})}\\=\lim_{n \to \infty}\frac{(\sqrt{n+1})^2-(\sqrt n)^2}{(\sqrt{n+1}+\sqrt{n})}\\=\lim_{n \to \infty}\frac{n+1-n}{(\sqrt{n+1}+\sqrt{n})}\\=\lim_{n \to \infty}\frac{1}{(\sqrt{n+1}+\sqrt{n})}\\=\lim_{x \to \infty}\frac{1/\sqrt{n}}{\sqrt{1+\frac 1n}+1}\\=0\,\,[\because \frac{1}{\sqrt n} \to 0\,\, \text{as}\,\,n \to \infty]\,\,\text{(proved)}$
$\,4(ii)\,\,\lim_{x \to \infty} \sqrt{x}[\sqrt{x+2}-\sqrt x]=1$
Sol. $\,\lim_{x \to \infty} \sqrt{x}[\sqrt{x+2}-\sqrt x]\\=\lim_{x \to \infty} \frac{ x[\sqrt{x+2}-\sqrt x][\sqrt{x+2}+\sqrt x]}{\sqrt x(\sqrt{x+2}+\sqrt x)}\\=\lim_{x \to \infty}\frac{x[(\sqrt{x+2})^2-(\sqrt x)^2]}{\sqrt x(\sqrt{x+2}+\sqrt x)}\\=\lim_{x \to \infty}\frac{x(x+2-x)}{\sqrt x(\sqrt{x+2}+\sqrt x)}\\=\lim_{x \to \infty}\frac{2x}{x\left(\sqrt{1+\frac 2x}+1\right)}\\=\frac{2}{1+1}~~~[\because \frac 1x \to 0\,\,\text{as}\,\, x\to \infty]\\=1\,\,\text{(proved)}$
$\,4.\,$ Prove
$\,(iii)\,\, \lim_{n \to \infty} [\sqrt{1+x+x^2}-x]=\frac 12$
Sol. $\,\lim_{n \to \infty}[\sqrt{1+x+x^2}-x]\\=\lim_{n \to \infty}\frac{(\sqrt{1+x+x^2}-x)(\sqrt{1+x+x^2}+x)}{(\sqrt{1+x+x^2}+x)}\\=\lim_{n \to \infty}\frac{(\sqrt{1+x+x^2})^2-(x)^2}{(\sqrt{1+x+x^2}+x)}\\=\lim_{n \to \infty}\frac{1+x+x^2-x^2}{(\sqrt{1+x+x^2}+x)}\\=\lim_{n \to \infty}\frac{1+x}{(\sqrt{1+x+x^2}+x)}\\=\lim_{x \to \infty}\frac{x\left(\frac 1x+1\right)}{x\left(\sqrt{\frac{1}{x^2}+\frac 1x+1}+1\right)}\\=\lim_{x \to \infty}\frac{\left(\frac 1x+1\right)}{\left(\sqrt{\frac{1}{x^2}+\frac 1x+1}+1\right)}\\=\frac{1}{1+1}\\=\frac 12\,\,\text{(proved)}$
4.Prove
$\,(iv)\,\,\lim_{n \to \infty} [\sqrt[3]{n+1}-\sqrt[3]{n}]=0$
Sol. $\,\,\,\lim_{n \to \infty} [\sqrt[3]{n+1}-\sqrt[3]{n}]\\=\lim_{n \to \infty }\frac{[\sqrt[3]{n+1}-\sqrt[3]{n}]\times [(n+1)^{\frac 23}+n^{\frac 13}(n+1)^{\frac 13}+n^{\frac 23}]}{[(n+1)^{\frac 23}+n^{\frac 13}(n+1)^{\frac 13}+n^{\frac 23}]}\\=\lim_{n \to \infty} \frac{\left(\sqrt[3]{n+1}\right)^3-\left(\sqrt[3]{n}\right)^3}{(n+1)^{\frac 23}+n^{\frac 13}(n+1)^{\frac 13}+n^{\frac 23}}\\=\lim_{n \to \infty}\frac{n+1-n}{(n+1)^{\frac 23}+n^{\frac 13}(n+1)^{\frac 13}+n^{\frac 23}}\\=\lim_{n \to \infty} \frac{1}{(n+1)^{\frac 23}+n^{\frac 13}(n+1)^{\frac 13}+n^{\frac 23}}\\=0\,\,[*]\,\,\text{(proved)}$
Note[*]: As $\,n \to \infty,\,\,$ Denominator $\to \infty.$



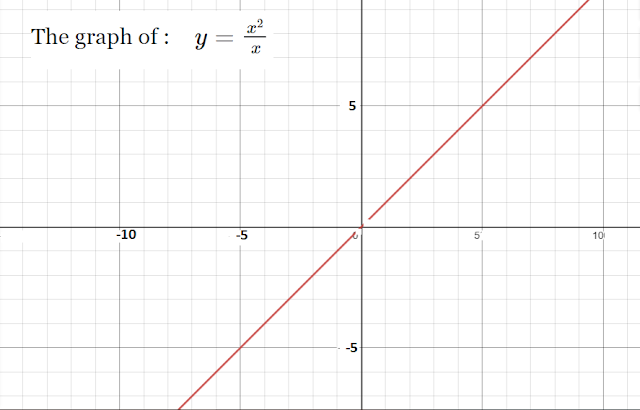







Please do not enter any spam link in the comment box