In the previous article, we have discussed Short Answer Type Questions and solutions of S N De Vector Algebra Chapter. In this article , we will solve the problems of Long Answer Type questions as given in the Chhaya Publication Book of Vector Chapter. So, let's start.
.png) |
| Vector Algebra (Part-3) | S N Dey | Class 12 |
$~1(i)~$ If $~\vec{a}=2\hat{i}+4\hat{j}-4\hat{k},~~\vec{b}=-5\hat{i}+4\hat{j}+2\hat{k}~$ and $~\vec{c}=3\hat{i}-3\hat{j}-2\hat{k}~$ , then find the magnitude of the vector $~\vec{a}+\vec{b}+2\vec{c}~$ and a unit vector in the direction of this vector.
Solution.
$~\vec{a}+\vec{b}+2\vec{c} \\= (2\hat{i}+4\hat{j}-4\hat{k})+(-5\hat{i}+4\hat{j}+2\hat{k})\\+2(3\hat{i}-3\hat{j}-2\hat{k}) \\= (2-5+6)\hat{i}+(4+4-6)\hat{j}\\+(-4+2-4)\hat{k}\\=3\hat{i}+2\hat{j}-6\hat{k} \\~\therefore~|\vec{a}+\vec{b}+2\vec{c}|\\=\sqrt{3^2+2^2+(-6)^2} \\= \sqrt{9+4+36}\\=\sqrt{49}\\=7$
Hence, a unit vector in the direction of the given vector is :
$=\frac{\vec{a}+\vec{b}+2\vec{c}}{|\vec{a}+\vec{b}+2\vec{c}|}=\frac 17(3\hat{i}+2\hat{j}-6\hat{k})~~\text{(ans.)}$
$~(ii)~$ If $~\vec{a}=\hat{i}+\hat{j}+\hat{k},~~\vec{b}=2\hat{i}-\hat{j}+3\hat{k}~$ and $~c=\hat{i}-2\hat{j}+\hat{k}~$ find a unit vector in a direction parallel to vector $~(2\vec{a}-\vec{b}+3\vec{c}).$
Solution.
$~2\vec{a}-\vec{b}+3\vec{c}\\=2(\hat{i}+\hat{j}+\hat{k})-(2\hat{i}-\hat{j}+3\hat{k})\\+3(\hat{i}-2\hat{j}+\hat{k})\\=(2-2+3)\hat{i}+(2+1-6)\hat{j}\\+(2-3+3)\hat{k}\\=3\hat{i}-3\hat{j}+2\hat{k}\\~\therefore~|2\vec{a}-\vec{b}+3\vec{c}|\\=\sqrt{3^2+(-3)^2+2^2}\\=\sqrt{9+9+4}\\=\sqrt{22}$
Hence, a unit vector in a direction parallel to vector $~(2\vec{a}-\vec{b}+3\vec{c})~$ is given by :
$=\frac{2\vec{a}-\vec{b}+3\vec{c}}{|2\vec{a}-\vec{b}+3\vec{c}|}=\frac{1}{\sqrt{22}}(3\hat{i}-3\hat{j}+2\hat{k})~~\text{(ans.)}$
$~2.~$ By vector method, show that the four points $~(7,2,-3),~(6,1,4),~(-3,-4,-1)~$ and $~(-2,-3,-8)~$ are the vertices of a parallelogram.
Solution.
$~\text{Let}~\vec{a}=7\hat{i}+2\hat{j}-3\hat{k},~\\~ \vec{b}=6\hat{i}+\hat{j}+4\hat{k},~\\~\vec{c}=-3\hat{i}-4\hat{j}-\hat{k},~\\ ~ \vec{d}=-2\hat{i}-3\hat{j}-8\hat{k}.$
$~\text{Now,}~\vec{AB}\\=\vec{b}-\vec{a}\\=(6\hat{i}+\hat{j}+4\hat{k})-(7\hat{i}+2\hat{j}-3\hat{k})\\=(6-7)\hat{i}+(1-2)\hat{j}+(4+3)\hat{k}\\=-\hat{i}-\hat{j}+7\hat{k}\rightarrow(1),~\\~~\vec{DC}\\=\vec{c}-\vec{d}\\=(-3\hat{i}-4\hat{j}-\hat{k})-(-2\hat{i}-3\hat{j}-8\hat{k})\\=(-3+2)\hat{i}+(-4+3)\hat{j}+(-1+8)\hat{k}\\=-\hat{i}-\hat{j}+7\hat{k}\rightarrow(2)$
Hence, from $~(1)~$ and $~(2)~$, it follows that $~~\vec{AB}=\vec{DC}.$
So, $~\vec{AB},~~\vec{DC}~~$ are parallel.
Again, $~~|\vec{AB}|=|\vec{CD}|$
$~\therefore~$ From the results shown above we can conclude that the four given points are the vertices of a parallelogram.
$~3.~$ Find a unit vector in direction parallel to the sum of the vectors $~\vec{a}=2\hat{i}+4\hat{j}-5\hat{k}~$ and $~\vec{b}=\hat{i}+2\hat{j}+3\hat{k}~$; find also the direction cosines of this vector.
Solution.
$~\vec{a}+\vec{b}\\=(2\hat{i}+4\hat{j}-5\hat{k})+(\hat{i}+2\hat{j}+3\hat{k})\\=3\hat{i}+6\hat{j}-2\hat{k}\\~\therefore~|\vec{a}+\vec{b}|\\=\sqrt{3^2+6^2+(-2)^2}\\=\sqrt{9+36+4}\\=\sqrt{49}\\=7.$
Hence, a unit vector in direction parallel to the sum of the given vectors is :
$=\frac{\vec{a}+\vec{b}}{|\vec{a}+\vec{b}|}=\frac 17(3\hat{i}+6\hat{j}-2\hat{k}) \rightarrow(1)$
Also, the direction cosines of this vector are given by :
$~\frac 37,~\frac 67,~-\frac 27~~[\text{By (1)}]$
$~4.~$ If $~\vec{a}=2\hat{i}-2\hat{j}+\hat{k},~\vec{b}=2\hat{i}+3\hat{j}+6\hat{k}~$ and $~\vec{c}=-\hat{i}+2\hat{k},~$ then find the magnitude and direction of the vector $~\vec{a}-\vec{b}+2\vec{c}.$
Solution.
$~\vec{a}-\vec{b}+2\vec{c}\\=(2\hat{i}-2\hat{j}+\hat{k})-(2\hat{i}+3\hat{j}+6\hat{k})\\~~~+2(-\hat{i}+2\hat{k})\\=(2-2-2)\hat{i}+(-2-3)\hat{j}+(1-6+4)\hat{k}\\=-2\hat{i}-5\hat{j}-\hat{k}\\~\therefore~|\vec{a}-\vec{b}+2\vec{c}|\\=\sqrt{(-2)^2+(-5)^2+(-1)^2}\\=\sqrt{4+25+1}\\=\sqrt{30} \rightarrow(1)$
From $~(1)~$ we get the magnitude of the given vector and if the vector makes an angle $~\alpha~$ with the positive direction of $~x$-axis ,
$~\cos\alpha=\frac{-2}{\sqrt{30}} \Rightarrow \alpha=\cos^{-1}\left(\frac{-2}{\sqrt{30}}\right).$
$~5.~$ The vectors $~\vec{a}~$ and $~\vec{b}~$ are non-collinear. Find for what value of $~x~$ , the vectors $~\vec{c}=(x-7)\vec{a}+2\vec{b}~$ and $~\vec{d}=(2x+1)\vec{a}-\vec{b}~$ are collinear.
Solution.
$~\because~$ the vectors $~\vec{c}~$ and $~\vec{d}~$ are collinear,
$~\vec{c}=m\vec{d}~[\text{where m is non-zero scalar}] \\ \therefore~(x-7)\vec{a}+2\vec{b} =m[(2x+1)\vec{a}-\vec{b}] \\ \text{or,}~ (x-7)\vec{a}-m(2x+1)\vec{a}+2\vec{b}+m\vec{b}=0 \\ \text{or,}~~ (x-7-2mx-m)\vec{a}+(m+2)\vec{b}=0 \rightarrow(1)$
Since, the vectors $~\vec{a}~$ and $~\vec{b}~$ are non-collinear, we get from $~(1),$
$~x-7-2mx-m=0,~~m+2=0 \Rightarrow m=-2\\ \therefore~x-7-2 \times (-2) \times x-(-2)=0 \\ \text{or,}~~ x-7+4x+2=0 \\ \text{or,}~~ 5x-5=0 \\ \text{or,}~~ x=\frac 55=1. $
$~6.~$ Given that the points with position vectors $~12\hat{i}-5\hat{j},~10\hat{i}+3\hat{j}~$ and $~x\hat{i}+11\hat{j}~$ are collinear, find $~x.$
Solution.
Let the position vectors of three points $~A,B,C~$ be $~12\hat{i}-5\hat{j},~10\hat{i}+3\hat{j}~$ and $~x\hat{i}+11\hat{j}~$ respectively.
$~\text{Now,}~\vec{AB}=(10\hat{i}+3\hat{j})-(12\hat{i}-5\hat{j})=-2\hat{i}+8\hat{j},\\~\vec{BC}\\=(x\hat{i}+11\hat{j})-(10\hat{i}+3\hat{j})\\=(x-10)\hat{i}+8\hat{j}.$
Since the points $~A,B,C~$ are collinear,
$~\vec{AB}=m\vec{BC}~~[\text{where m is non-zero scalar}] \\ \therefore~ -2\hat{i}+8\hat{j}=m[(x-10)\hat{i}+8\hat{j}]\rightarrow(1)$
Now, comparing both sides of $~(1),~$ we get,
$~-2=m(x-10),~~8=8m \Rightarrow m=\frac 88=1 \\ \text{or,}~~ -2=1(x-10)\\~~\Rightarrow x=-2+10=8 ~\text{(ans.)}$
$~7.~$ The vectors $~\vec{a}~$ and $~\vec{b}~$ are non-collinear. If $~\vec{p}=(x+4y)\vec{a}+(2x+y+1)\vec{b}~$ and $~~\vec{q}=(-2x+y+2)\vec{a}+(2x-3y-1)\vec{b}~$ satisfy the relation $~3\vec{p}=2\vec{q}~$, find the values of $~x~$ and $~y.$
Solution.
$~ 3\vec{p}=2\vec{q} \\ \therefore~3[(x+4y)\vec{a}+(2x+y+1)\vec{b}] \\~=2[(-2x+y+2)\vec{a}+(2x-3y-1)\vec{b}] \\ \text{or,}~~(3x+12y)\vec{a}+(6x+3y+3)\vec{b}\\~=(-4x+2y+4)\vec{a}+(4x-6y-2) \vec{b}\rightarrow(1) $
Comparing both sides of $~(1),~$ we get,
$~ 3x+12y=-4x+2y+4 \\ \text{or,}~~ 7x+10y-4=0 \rightarrow(2) $
Again, by $~(1),~$
$~ 6x+3y+3=4x-6y-2 \\ \text{or,}~~ 2x+9y+5=0 \rightarrow(3)$
Hence, from $~(2),~(3)~$ we get by cross-multiplication method,
$~~\frac{x}{50-(-36)}=\frac{y}{-8-35}=\frac{1}{63-20} \\ \text{or,}~~\frac{x}{86}=\frac{y}{-43}=\frac{1}{43} \\ \therefore~ x=\frac{86}{43}=2,~~y=\frac{-43}{43}=-1. $
Objective Physics, Chemistry & Mathematics Chapter-wise Practice Question Bank for NTA JEE Main/ BITSAT 4th Edition | MCQs & NVQs based on Main ... PYQs | Useful for CBSE 11/ 12 & CUET | PCM Paperback
$~8.~$ If the sum of two unit vectors is a unit vector , prove that the magnitude of their difference is $~\sqrt{3}.$
Solution.
Let $~\vec{a}~$ and $~\vec{b}~$ be two vectors so that their sum $~(\vec{a}+\vec{b})~$ is also a unit vector.
$~\therefore~ |\vec{a}|=1=|\vec{b}|,~~|\vec{a}+\vec{b}|=1 \rightarrow(1)$
Now, we know that
$~ |\vec{a}+\vec{b}|^2+|\vec{a}-\vec{b}|^2 = 2(|\vec{a}|^2+|\vec{b}|^2) \\ ~\therefore~ 1^2+|\vec{a}-\vec{b}|^2=2(1^2+1^2) \\ \text{or,}~~ 1+|\vec{a}-\vec{b}|^2=2(1+1) \\ \text{or,}~~ 1+|\vec{a}-\vec{b}|^2=2 \times 2 \\ \text{or,}~~ |\vec{a}-\vec{b}|^2=4-1 \\ \therefore~ |\vec{a}-\vec{b}|=\sqrt{3} ~~\text{(proved)}$
TARGET JEE Advanced 2023 - 10 Previous Year Solved Papers (2013 - 2022) & 5 Mock Tests Papers 1 & 2 - 17th Edition | Answer Key validated with IITJEE JAB | PYQs Question Bank | Paperback
$~9.~~ ABCDEF~$ is a regular hexagon. If $~ \vec{CD}=\vec{a},~~\vec{DE}=\vec{b}, ~$ find $~ \vec{BC},~\vec{BF},~ \vec{CA},~\vec{AD}~$ and $~ \vec{BD}~$ in terms of $~\vec{a}~$ and $~\vec{b}.$
Solution.
We have, $~\vec{CD}=\vec{a},~~\vec{DE}=\vec{b}.~$
$~\therefore~\vec{AB}=\vec{ED}=-\vec{b} \rightarrow(1)$
$\text{From}~ \Delta CDE, \\ ~ ~ \vec{CE}=\vec{CD}+\vec{DE}=\vec{a}+\vec{b} ~~[\text{By (1)}]$
$\text{Again,}~ \vec{CE} \parallel \vec{BF} \\ ~\therefore~ \vec{BF}=\vec{a}+\vec{b}$
$~\text{Again, from}~ \Delta BCE, ~\\~~ \vec{BC}+\vec{CE}=\vec{BE} \\~ \therefore~ \vec{BC}=\vec{BE}-\vec{CE} \\ \text{or,}~~ \vec{BC}=2 \cdot \vec{CD}-(\vec{a}+\vec{b}) \\ \text{or,}~~ \vec{BC}=2\vec{a}-\vec{a}-\vec{b} \\ \text{or,}~~ \vec{BC}=\vec{a}-\vec{b}$
$\text{From}~~\Delta ABC, ~\\~~ vec{AB}+\vec{BC}=\vec{AC} \\ \therefore~ -\vec{b}+\vec{a}-\vec{b}=\vec{AC} \\ \text{or,}~~ \vec{AC}=\vec{a}-2\vec{b} \\ \text{or,}~~ \vec{CA}=-(\vec{a}-2\vec{b})=2\vec{b}-\vec{a}. $
$\text{From}~ \Delta ACD,~~\\~~ \vec{AC}+\vec{CD}=\vec{AD} \\ \therefore~ \vec{AD}=\vec{AB}+\vec{BC}+\vec{CD}=-\vec{b}+\vec{a}-\vec{b}+\vec{a} \\ \text{or,}~~ \vec{AD}=2\vec{a}-2\vec{b} \\ \text{or,}~~ \vec{AD}=2(\vec{a}-\vec{b}). $

$\text{From}~ \Delta BCD, ~~\vec{BC}+\vec{CD}=\vec{BD} \\ \therefore~ \vec{a}-\vec{b}+\vec{a}=\vec{BD} \\ \text{or,}~~ \vec{BD}=2\vec{a}-\vec{b}.$
$~10.~~\overline{AC}~$ and $~\overline{BD}~$ are the diagonals of the parallelogram $~ABCD~$ . Prove that , $~\vec{AC}+\vec{BD}=2\vec{BC}~$ and $~\vec{AC}-\vec{BD}=2\vec{AB}.$
Solution.
From $~\Delta ABC,~$ we get ( by using triangle law of addition of vectors ),
$~ \vec{AC}=\vec{AB}+\vec{BC}\rightarrow(1.0) \\~\therefore~ \vec{BC}=\vec{AC}-\vec{AB}\rightarrow(1)$
Again, from $~\Delta ABD,~$ we get ( by using triangle law of addition of vectors ),
$~ \vec{AD}=\vec{AB}+\vec{BD}\rightarrow(1.1) \\ ~\therefore~ \vec{BC}=\vec{AB}+\vec{BD}~[*]\rightarrow(2)$
Note [*] : $~~\because~ \vec{AD}=\vec{BC} ~$ as $~ABCD~$ is a parallelogram.
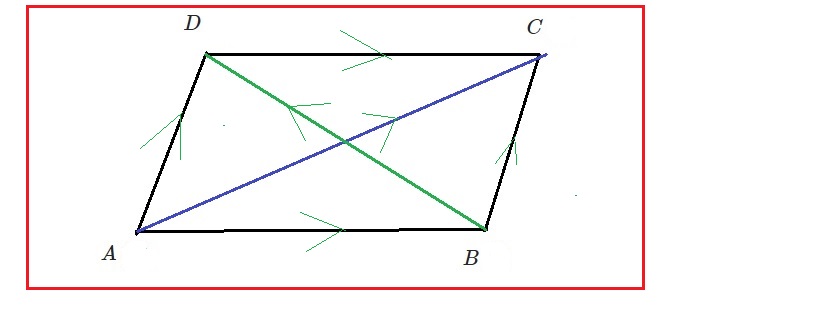
Now by adding $~(1)~$ and $~(2)~$, we get
$~ \vec{BC}+\vec{BC}=(\vec{AC}-\vec{AB})+(\vec{AB}+\vec{BD}) \\ \therefore 2\vec{BC}=\vec{AC}+\vec{BD}~~\text{(proved)}$
$~\text{Again,}~ \vec{AC}-\vec{BD}\\=(\vec{AB}+\vec{BC})-(\vec{AD}-\vec{AB})\\~~~~[\text{By (1.0), (1.1)}] \\=(\vec{AB}+\vec{BC})-(\vec{BC}-\vec{AB})~\\~~ [~\because~\vec{AD}=\vec{BC}] \\=\vec{AB}+\vec{BC}-\vec{BC}+\vec{AB}\\=2\vec{AB} ~\text{(proved)}$











Please do not enter any spam link in the comment box