In this article, we will discuss the solutions of Very Short Answer Type Questions in the chapter Product of Two Vectors as given in the Chhaya Publication Book of aforementioned chapter of S N De book. In the previous article, we have discussed Vector . So, let’s start.
Vector Product related solutions of S N Dey mathematics Class 12 of Ex-2A
$~1.~$ Define scalar product of two vectors. Show that scalar product of vectors satisfies the commutative and distributive laws.
Solution.
The scalar product (or dot product) of two vectors $~\vec{a}~$ and $~\vec{b}~$ is denoted by $~\vec{a} \cdot \vec{b}~;~$ It is a scalar and is defined as follows :
$~\vec{a} \cdot\vec{b}=|\vec{a}||\vec{b}| \cos\theta~,~$ where $~\theta~$ is the angle between the vectors $~\vec{a}~$ and $~\vec{b}~$ and $~|\vec{a}|,~|\vec{b}|~$ are the moduli of the vectors $~\vec{a}~$ and $~\vec{b}~$ respectively.
Since $~~\cos\theta >0~$ when $~\theta~$ is acute and $~\cos\theta<0~$ when $~\theta~$ is obtuse, it follows that the scalar product $~\vec{a} \cdot\vec{b}~$ is positive when $~\theta~$ is acute and negative when $~\theta~$ is obtuse .
2nd part :
Scalar product is commutative :
$\text{We have,}~~ \vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\cos\theta, \\~~~\\~~~ ~~~~~~\vec{b}\cdot \vec{a}=|\vec{b}||\vec{a}|\cos\theta $
Since $~~|\vec{a}||\vec{b}|=|\vec{b}||\vec{a}|,~~$ it follows that $~~\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}$
Scalar Product is distributive with respect to vector addition :
Let $~~ \vec{OA}=\vec{a},~~ \vec{OB}=\vec{b},~~\vec{BC}=\vec{c}~~$ where $~|\vec{a}|=\overline{OA},~~|\vec{b}|=\overline{OB},~~ |\vec{c}|=\overline{BC}.$
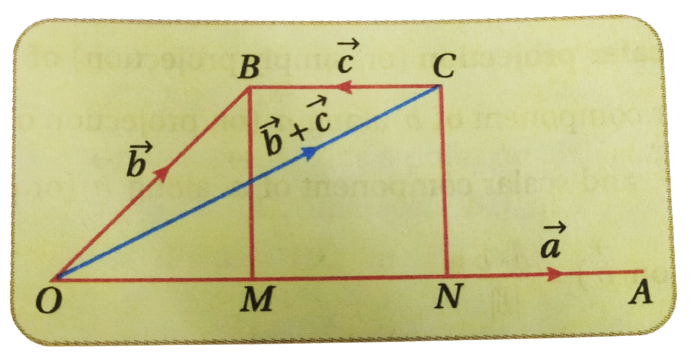
From the points $~B~$ and $~C~$ we draw perpendiculars $~BM~$ and $~CN~$ on $~OA~$. In addition law of vectors we get,
$~~\vec{b}+\vec{c}=\vec{OB}+\vec{BC}=\vec{OC}. \\ \therefore~~ \vec{a} \cdot (\vec{b}+\vec{c}) \\=|\vec{a}|~~[\text{scalar component of} ~~(\vec{b}+\vec{c})~~\text{along}~~\vec{a} ] \\= |\vec{a}|\overline{ON} \\= |\vec{a}| ( \overline{OM}+\overline{MN})\\= |\vec{a}|\overline{OM}+|\vec{a}|\overline{MN} \\= |\vec{a}|(\text{scalar component of}~~\vec{b}~~\text{along}~~\vec{a}) \\+ |\vec{a}|(\text{scalar component of} ~~\vec{c}~~\text{along}~~\vec{a})\\= \vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}.$
$~2.~$ Find the scalar product of the following pair of vectors and the angle between them :
$~(i)~~\hat{i}+\hat{j}~$ and $~\hat{j}+\hat{k}$
Solution.
$~~(\hat{i}+\hat{j}) \cdot (\hat{j}+\hat{k})\\~~~=\hat{i}\cdot \hat{j}+\hat{i} \cdot \hat{k}+\hat{j}\cdot \hat{j}+\hat{j} \cdot \hat{k}\\~~~=0+0+1+0~~[*]\\~~~=1\rightarrow(1)$
Note [*] : $~~\hat{j}\cdot \hat{j}=|\hat{j}||\hat{j}| \cos 0=1 \cdot 1 \cdot 1=1$
If $~~\theta~~$ be the angle between two given vectors then
$~ ~\cos\theta=\frac{(\hat{i}+\hat{j}) \cdot (\hat{j}+\hat{k})}{|\hat{i}+\hat{j}||\hat{j}+\hat{k}|}=\frac{1}{\sqrt{1^2+1^2} \sqrt{1^2+1^2}}~~[\text{By (1)}] \\~\therefore~ \cos\theta=\frac{1}{\sqrt{2}\sqrt{2}}=\frac 12=\cos(\pi/3) \\ \text{or,}~~ \theta=\frac{\pi}{3}~~\text{(ans.)}$
$~~(ii)~~2\hat{i}-\hat{j}+2\hat{k}~~$ and $~~\hat{i}+\hat{j}+\hat{k} .$
Solution.
$(2\hat{i}-\hat{j}+2\hat{k}) \cdot (\hat{i}+\hat{j}+\hat{k})\\=2+(-1)+2~~[*]\\=3\rightarrow(1)$
$\text{Note[*] :}~~ \hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k}\cdot \hat{k}=1,\\~~~~~~\hat{i} \cdot \hat{j}=\hat{i} \cdot \hat{k}=\hat{j} \cdot \hat{i}=\hat{j} \cdot \hat{k}=\cdots=0$
If $~~\theta~~$ be the angle between two given vectors then
$~\cos\theta\\=\frac{(2\hat{i}-\hat{j}+2\hat{k}) \cdot (\hat{i}+\hat{j}+\hat{k})}{|2\hat{i}-\hat{j}+2\hat{k}||\hat{i}+\hat{j}+\hat{k}|}\\=\frac{3}{\sqrt{2^2+(-1)^2+2^2} \sqrt{1^2+1^2+1^2}}~~[\text{By (1)}] \\ ~\therefore~~\cos\theta=\frac{3}{\sqrt{9}\sqrt{3}}=\frac{3}{3\sqrt{3}} \\ \text{or,}~~ \cos\theta=\frac{1}{\sqrt{3}} \\ \text{or,}~~ \theta=\cos^{-1}\left(\frac{1}{\sqrt{3}}\right)~~\text{(ans.)}$
$~(iii)~~\vec{a}=2\hat{i}+3\hat{j}-4\hat{k}~~$ and $~~\vec{b}=\hat{i}+2\hat{j}+\hat{k}.$
Solution.
$\vec{a} \cdot \vec{b}=(2\hat{i}+3\hat{j}-4\hat{k}) \cdot (\hat{i}+2\hat{j}+\hat{k}) \\ \therefore~ \vec{a} \cdot \vec{b}=2+3 \times 2+(-4) \times 1 \\ \text{or,}~~ \vec{a} \cdot \vec{b}=2+6-4=4 \rightarrow(1)$
$~[\because~~\hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1, \\~~~~~ \hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0 ~]$
$~|\vec{a}|\\=\sqrt{2^2+3^2+(-4)^2}\\=\sqrt{4+9+16}\\=\sqrt{29},\\~~~~~~|\vec{b}|\\=\sqrt{1^2+2^2+1^2}\\=\sqrt{1+4+1}\\=\sqrt{6} \rightarrow(2)$
If $~~ \theta ~~$ be the angle between two given vectors then
$\cos\theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\frac{4}{\sqrt{29} \sqrt{6}} ~~[\text{By (1),(2)}] \\ \text{or,}~~ \cos\theta=\frac{4}{\sqrt{174}} \\ \therefore~ \theta=\cos^{-1}\left(\frac{4}{\sqrt{174}}\right). $
(iv) $~ \vec{a}=2\hat{i}-5\hat{j}+3\hat{k}~~$ and $~~ \vec{b}=\hat{i}-2\hat{j}-4\hat{k}.$
Solution.
$~ \vec{a} \cdot \vec{b}\\=(2\hat{i}-5\hat{j}+3\hat{k}) \cdot (\hat{i}-2\hat{j}-4\hat{k})\\=2 \times 1+(-5)\times (-2)+3 \times (-4)\\=2+10-12\\=0\rightarrow(1)$
$~[~\because~~ \hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1, ~~\hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0~]$
If $~~\theta~~$ be the angle between two given vectors then
$~~ \cos\theta=\frac{\vec{a}\cdot \vec{b}}{|\vec{a}||\vec{b}|}=\frac{0}{|\vec{a}||\vec{b}|}\\ \text{or,}~~ \cos\theta=0=\cos(\pi/2) \\ \therefore~\theta=\frac{\pi}{2}~~\text{(ans.)}$
3(i) Show that the vectors $~~\vec{a}=2\hat{i}+\hat{j}-\hat{k}~~$ and $~~ \vec{b}=\hat{i}+\hat{j}+3\hat{k}~~$ are perpendicular to each other.
Solution.
Two vectors $~~\vec{a}~~$ and $~~\vec{b}~~$ are perpendicular to each other if $~~\vec{a} \cdot \vec{b}=0 \rightarrow(1)$
$~\vec{a} \cdot \vec{b}\\=(2\hat{i}+\hat{j}-\hat{k}) \cdot (\hat{i}+\hat{j}+3\hat{k})\\=2+1-3\\=0 \rightarrow(2)$
Hence, by $~(1),~(2)~$ we can conclude that two given vectors are perpendicular to each other.
Show that the vectors $~(ii)~~\vec{a}=(3,2,-1)~~$ and $~~\vec{b}=(-2,0,-6)~~$ are perpendicular to each other.
Solution.
$~\vec{a}=(3,2,-1)=3\hat{i}+2\hat{j}-\hat{k},\\~~~~~~\vec{b}=(-2,0,-6)=-2\hat{i}-6\hat{k}\\ ~\therefore~\vec{a} \cdot \vec{b}\\=(3\hat{i}+2\hat{j}-\hat{k}) \cdot (-2\hat{i}-6\hat{k})\\=3 \times (-2) +2 \times 0+(-1) \times (-6)\\=-6+6\\=0 \rightarrow(1)$
Hence by $~(1)~$ we can conclude that the two given vectors are perpendicular to each other.
Show that the vectors $~~(iii)~~ \vec{\alpha}=-3\hat{i}-2\hat{j}+\hat{k}~~$ and $~~\vec{\beta}=-2\hat{i}+\hat{j}-4\hat{k}~~$ are perpendicular to each other.
Solution.
$\vec{\alpha} \cdot \vec{\beta}\\=(-3\hat{i}-2\hat{j}+\hat{k}) \cdot (-2\hat{i}+\hat{j}-4\hat{k})\\=(-3)\times (-2)+(-2) \times 1+1 \times (-4)\\=6-2-4\\=0\rightarrow(1)$
Hence by $~(1)~$ we can conclude that the two given vectors are perpendicular to each other.
4. Show that the vectors $~~ (i)~~ \hat{i}+2\hat{j}+\hat{k},~\hat{i}+\hat{j}-3\hat{k}~~$ and $~~7\hat{i}-4\hat{j}+\hat{k}~~$ are perpendicular to each other.
Solution.
$~\vec{a}=\hat{i}+2\hat{j}+\hat{k},~~\vec{b}=\hat{i}+\hat{j}-3\hat{k},\\~~\vec{c}=7\hat{i}-4\hat{j}+\hat{k}$
$~\therefore~~\vec{a} \cdot \vec{b}\\=(\hat{i}+2\hat{j}+\hat{k}) \cdot (\hat{i}+\hat{j}-3\hat{k})\\=1+2-3=0 \rightarrow(1)\\~~\\~~~ \vec{b} \cdot \vec{c}\\=(\hat{i}+\hat{j}-3\hat{k}) \cdot (7\hat{i}-4\hat{j}+\hat{k})\\=7+1 \times (-4)+(-3) \times 1\\=7-4-3=0\rightarrow(2)\\~~\\~~ \vec{c} \cdot \vec{a}\\=(7\hat{i}-4\hat{j}+\hat{k}) \cdot (\hat{i}+2\hat{j}+\hat{k})\\=7+(-4) \times 2+1 \times 1\\=7-8+1=0 \rightarrow(3)$
From $~(1),~(2),~(3)~$ it follows that $~~\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{c}=\vec{c} \cdot \vec{a}=0$
Hence, the three given vectors are perpendicular to each other.
4(ii) Show that the vectors $~~\vec{a}=2\hat{i}+3\hat{j}+6\hat{k}~,~\vec{b}=3\hat{i}-6\hat{j}+2\hat{k}~~$ and $~~\vec{c}=6\hat{i}+2\hat{j}-3\hat{k}~~$ are mutually perpendicular.
Solution.
$~\vec{a} \cdot \vec{b}\\=(2\hat{i}+3\hat{j}+6\hat{k}) \cdot (3\hat{i}-6\hat{j}+2\hat{k}) \\= 2 \times 3+3 \times (-6)+ 6 \times 2\\= 6-18+12=0 \rightarrow(1),\\~~\\~~~~\vec{b}\cdot \vec{c}\\=(3\hat{i}-6\hat{j}+2\hat{k}) \cdot (6\hat{i}+2\hat{j}-3\hat{k})\\= 3 \times 6+(-6) \times 2+2 \times (-3)\\= 18-12-6=0 \rightarrow(2)\\~~\\~~~~\vec{c}\cdot \vec{a}\\=(6\hat{i}+2\hat{j}-3\hat{k}) \cdot (2\hat{i}+3\hat{j}+6\hat{k})\\=6 \times 2+2 \times 3+(-3) \times 6\\=12+6-18=0 \rightarrow(3)$
From $~(1),~(2),~(3)~$ it follows that $~~\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{c}=\vec{c} \cdot \vec{a}=0$
Hence, the three given vectors are perpendicular to each other.
5. In each of the following cases two vectors are perpendicular to each other , find $~m.$
$~(i)~~ m\hat{i}-2\hat{j}+\hat{k}~~$ and $~~ 3\hat{i}-2\hat{j}-7\hat{k} .$
Solution.
let $~~\vec{a}=m\hat{i}-2\hat{j}+\hat{k} ,~~\vec{b}=3\hat{i}-2\hat{j}-7\hat{k}$
For two vectors $~~\vec{a},~~\vec{b}$ to be perpendicular to each other , we must have $~~\vec{a} \cdot \vec{b}=0 \\ \text{or,}~~ (m\hat{i}-2\hat{j}+\hat{k}) \cdot (3\hat{i}-2\hat{j}-7\hat{k})=0 \\ \text{or,}~~ 3m+(-2)\times (-2)+1 \times (-7)=0 \\ \text{or,}~~ 3m+4-7=0 \\ \text{or,}~~ 3m-3=0 \\ \text{or,}~~ 3m=3 \\ \text{or,}~~ m=\frac 33=1~~\text{(ans.)} $
$~(ii)~~ \vec{a}=2\hat{j}-5\hat{k}~~$ and $~~\vec{b}=-3\hat{i}-m\hat{j}+4\hat{k}$
Solution.
We have, $~\vec{a}=2\hat{j}-5\hat{k} ,~~\vec{b}=-3\hat{i}-m\hat{j}+4\hat{k}$
For two vectors $~~\vec{a},~~\vec{b}~~$ to be perpendicular to each other , we must have
$~\vec{a} \cdot \vec{b}=0 \\ \text{or,}~~ (2\hat{j}-5\hat{k}) \cdot (-3\hat{i}-m\hat{j}+4\hat{k})=0 \\ \text{or,}~~ 0+2 \times (-m)+(-5) \times 4=0 \\ \text{or,}~~ -2m-20=0 \\ \text{or,}~~ -2(m+10)=0 \\ \text{or,}~~ m+10=0\\ \text{or,}~~ m=-10 ~~ \text{(ans.)} $
$~(iii)~~\vec{a}=(1,1,m)~~$ and $~~\vec{b}=(4,m,-3).$
Solution.
We have $~~ \vec{a}=\hat{i}+\hat{j}+m\hat{k},~~\vec{b}=4\hat{i}+m\hat{j}-3\hat{k} .$
For two vectors $~~\vec{a},~~\vec{b}~~$ to be perpendicular to each other , we must have
$~\vec{a} \cdot \vec{b} =0 \\ \text{or,}~~ (\hat{i}+\hat{j}+m\hat{k}) \cdot (4\hat{i}+m\hat{j}-3\hat{k})=0 \\ \text{or,}~~ 4+m-3m=0 \\ \text{or,}~~ 4-2m=0\\ \text{or,}~~ 4=2m\\ \text{or,}~~ 2m=4 \\ \text{or,}~~ m=\frac 42=2~~\text{(ans.)} $
6. If $~\vec{a}=\hat{i}+2\hat{j}-3\hat{k}~~$ and $~~\vec{b}=3\hat{i}-\hat{j}+2\hat{k}~~$ then show that the vectors $~~(\vec{a}+\vec{b})~~$ and $~~(\vec{a}-\vec{b})~~$ are perpendicular to each other.
Solution.
$~~\vec{a}+\vec{b}\\=(\hat{i}+2\hat{j}-3\hat{k})+(3\hat{i}-\hat{j}+2\hat{k})\\=4\hat{i}+\hat{j}-\hat{k} \rightarrow(1)$
$~\text{Again,}~~\vec{a}-\vec{b}\\=(\hat{i}+2\hat{j}-3\hat{k})-(3\hat{i}-\hat{j}+2\hat{k})\\=-2\hat{i}+3\hat{j}-5\hat{k}\rightarrow(2)$
$~\text{Now,}~~(\vec{a}+\vec{b}) \cdot (\vec{a}-\vec{b})\\=(4\hat{i}+\hat{j}-\hat{k}) \cdot (-2\hat{i}+3\hat{j}-5\hat{k})~~[\text{By (1),(2)}]\\=-8+3+5\\=0 \rightarrow(3)$
Hence, by $~(3)~$ we can conclude that the vectors $~~(\vec{a}+\vec{b})~~$ and $~~(\vec{a}-\vec{b})~~$ are perpendicular to each other.
7. If $~~\vec{a}=3\hat{i}+2\hat{j}+9\hat{k}~~$ and $~~\vec{b}=\hat{i}+\lambda \hat{j}+3\hat{k}~,~$ then find the value of $~~\lambda~,~$ so that the vectors $~~(\vec{a}+\vec{b})~~$ and $~~(\vec{a}-\vec{b})~~$ are perpendicular to each other.
Solution.
$\vec{a}+\vec{b} \\= (3\hat{i}+2\hat{j}+9\hat{k})+(\hat{i}+\lambda \hat{j}+3\hat{k}) \\ =4\hat{i}+(2+\lambda)\hat{j}+12\hat{k}, ~\\~~\\~~~ \vec{a}-\vec{b}\\=(3\hat{i}+2\hat{j}+9\hat{k})-(\hat{i}+\lambda \hat{j}+3\hat{k}) \\=2\hat{i}+(2-\lambda)\hat{j}+6\hat{k} $
If the vectors $~~(\vec{a}+\vec{b})~~$ and $~~(\vec{a}+\vec{b})~~$ are perpendicular to each other, then
$(\vec{a}+\vec{b}) \cdot (\vec{a}-\vec{b})=0\\ \text{or,}~~ [4\hat{i}+(2+\lambda)\hat{j}+12\hat{k}] \cdot [2\hat{i}+(2-\lambda)\hat{j}+6\hat{k}]=0 \\ \text{or,}~~ 4 \times 2+(2+\lambda)(2-\lambda)+72=0 \\ \text{or,}~~ 8+2^2-\lambda^2+72=0 \\ \text{or,}~~ 84-\lambda^2=0 \\ \text{or,}~~ 84=\lambda^2 \\ \text{or,}~~ \lambda^2=84 \\ \text{or,}~~ \lambda=\pm \sqrt{84}=\pm\sqrt{4 \times 21}=\pm 2\sqrt{21} ~~\text{(ans.)}$
8. If $~~\vec{a}=2\hat{i}-\hat{j}+3\hat{k}~~$ and $~~\vec{b}=3\hat{i}+\hat{j}-2\hat{k}~,~~$ find the angle between the vectors $~~(\vec{a}+\vec{b})~~~$ and $~~(\vec{a}-\vec{b})~.$
Solution.
$\vec{a}+\vec{b}\\= (2\hat{i}-\hat{j}+3\hat{k})+(3\hat{i}+\hat{j}-2\hat{k})\\=5\hat{i}+\hat{k},\\~~ \\ \therefore~~|\vec{a}+\vec{b}|\\=\sqrt{5^2+1^2}\\=\sqrt{25+1}=\sqrt{26} \\~~\\~~ \vec{a}-\vec{b} \\= (2\hat{i}-\hat{j}+3\hat{k})-(3\hat{i}+\hat{j}-2\hat{k}) \\=-\hat{i}-2\hat{j}+5\hat{k}\\~~ \\~\therefore~~ |\vec{a}-\vec{b}|\\=\sqrt{(-1)^2+(-2)^2+5^2}\\=\sqrt{1+4+25}=\sqrt{30}.$
$\text{Also,}~~ (\vec{a}+\vec{b})\cdot (\vec{a}-\vec{b}) \\= (5\hat{i}+0\cdot \hat{j}+\hat{k})\cdot (-\hat{i}-2\hat{j}+5\hat{k}) \\= -5+0+5=0 $
If $~~\theta~~$ is the angle between the vectors $~~(\vec{a}+\vec{b})~~$ and $~~(\vec{a}-\vec{b}),~~$ then
$\cos\theta=\frac{(\vec{a}+\vec{b}) \cdot (\vec{a}-\vec{b})}{|\vec{a}+\vec{b}||\vec{a}+\vec{b}|}=\frac{0}{\sqrt{26} \sqrt{30}} \\ \therefore \cos\theta=0=\cos(\pi/2) \\ \text{or,}~~\theta=\frac{\pi}{2}~~\text{(ans.)}$
9. Find the scalar and vector components of $~~\vec{a}~~$ in the direction of $~~\vec{b}~~$ where $~~(i)~~\vec{a}=\hat{i}+\hat{j}~~$ and $~~\vec{b}=\hat{j}+\hat{k}.$
Solution.
$~\vec{a} \cdot \vec{b}=(\hat{i}+\hat{j}) \cdot (\hat{j}+\hat{k})=1\\~~~\\~~|\vec{b}|=\sqrt{1^2+1^2}=\sqrt{2}$
The scalar component of $~~\vec{a}~~$ in the direction of $~~\vec{b}~~$ is :
$\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}=\frac{1}{\sqrt{2}}~~\text{(ans.)}$
The vector components of $~~\vec{a}~~$ in the direction of $~~\vec{b}~~$ is given by :
$=\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|^2} (\vec{b}) \rightarrow(1)$
So, by $~(1)~$ we get,
$\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|^2} (\vec{b})=\frac{1}{(\sqrt{2})^2} (\hat{j}+\hat{k})=\frac 12(\hat{j}+\hat{k})~~\text{(ans.)}$
Find the scalar and vector components of $~~\vec{a}~~$ in the direction of $~~\vec{b}~~$ where $~~(ii)~~ \vec{a}=3\hat{i}+\hat{j}+3\hat{k}~~$ and $~~\vec{b}=\hat{i}-\hat{j}-\hat{k}.$
Solution.
$\vec{a} \cdot \vec{b} \\ =(3\hat{i}+\hat{j}+3\hat{k}) \cdot (\hat{i}-\hat{j}-\hat{k}) \\= 3-1-3=-1 \\~~\\~~ |\vec{b}|=\sqrt{1^2+(-1)^2+(-1)^2}=\sqrt{3}$
The scalar components of $~~\vec{a}~~$ in the direction of $~~\vec{b}~~$ is given by :
$\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}=\frac{-1}{\sqrt{3}}~~\text{(ans.)}$
Since the scalar component is negative , so the unit vector of $~~\vec{b}~~$ is negative on vector component and so the vector component of $~~\vec{a}~~$ in the direction of $~~\vec{b}~~$ is given by :
$=\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|} \left(-\frac{\vec{b}}{|\vec{b}|}\right) \rightarrow(1)$
So, by $~(1)~$ we get,
$\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|} \left(-\frac{\vec{b}}{|\vec{b}|}\right)\\=\frac{-1}{\sqrt{3}} \left(\frac{-(\hat{i}-\hat{j}-\hat{k})}{\sqrt{3}}\right)\\=\frac 13(\hat{i}-\hat{j}-\hat{k})~~\text{(ans.)}$
10. Find the scalar and vector projection of $~~\vec{b}~~$ on $~~\vec{a}~~$ where $~~\vec{a}=\hat{i}+2\hat{j}+2\hat{k}~~$ and $~~\vec{b}=\hat{j}+2\hat{k}.$
Solution.
$\vec{a} \cdot \vec{b}\\=(\hat{i}+2\hat{j}+2\hat{k}) \cdot (\hat{j}+2\hat{k})\\=0+2+4=6$
$|\vec{a}|=\sqrt{1^2+2^2+2^2}=\sqrt{1+4+4}=\sqrt{9}=3$
Now, the scalar projection of $~~\vec{b}~~$ on $~~\vec{a}~~$ is given by :
$=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}|^2} (\vec{a})\\~~~~=\frac{6}{3^2}(\hat{i}+2\hat{j}+2\hat{k})\\~~~~=\frac 69(\hat{i}+2\hat{j}+2\hat{k})\\~~~~=\frac 23(\hat{i}+2\hat{j}+2\hat{k})~~\text{(ans.)}$


.png)







Please do not enter any spam link in the comment box