In the previous article, we finished the remaining short answer type questions of Straight Line Chapter of Chhaya Mathematics , Class 11. In this article, we have solved $~9~$ Long Answer Type Questions.
1. A straight line passes through the point $~(2,3)~$ and is such that the sum of its intercepts on the co-ordinate axes is $~10.~$ Find the equation of the straight line.
Solution.
The equation of the straight line in intercept form is $~\frac xa+\frac yb=1~$ where $~a=x-$intercept and $~b=y-$intercept of the line.
According to the problem, $~a+b=10\rightarrow(1)$ and since the straight line passes through $~(2,3)~$, so
$~\frac 2a+\frac 3b=1 \\ \text{or,}~~ \frac 2a+\frac{3}{10-a}=1\rightarrow [\text{By (1)}] \\ \text{or,}~~ \frac{2(10-a)+3a}{a(10-a)}=1 \\ \text{or,}~~ 20+a=10a-a^2 \\ \text{or,}~~ a^2-10a+a+20=0 \\ \text{or,}~~ a^2-9a+20=0 \\ \text{or,}~~ a^2-5a-4a+20=0 \\ \text{or,}~~ a(a-5)-4(a-5)=0 \\ \text{or,}~~ (a-4)(a-5)=0 \\ \text{or,}~~ a=4,5$
For $~a=4,5~$ the respective values of $~b=10-4=6,~ 10-5=5.$
Hence, the required equation of the straight line is
$~\frac x4+\frac y6=1 \Rightarrow 3x+2y=12,\\~ \frac x5+\frac y5=1 \Rightarrow x+y=5.$
2. Two straight lines drawn through the origin, trisect the portion of the line $~4x+3y=12~$ intercept between the axes. Find the equations of the straight lines.
Solution.
$\because~ CA : AD=1:2,~\\~~ A\equiv \left(\frac{1 \cdot 3+ 2 \cdot 0}{1+2},\frac{1 \cdot 0+2 \cdot 4}{1+2}\right)=(1,\frac 83)$
Again, $~ CB : BD=2 :1,~\\~B \equiv \left(\frac{2 \cdot 3+1 \cdot 0}{2+1},\frac{2 \cdot 0+1 \cdot 4}{2+1}\right)=(2,\frac 43)$
$\therefore~$ the equation of $~OA~$ is :
$~y=\frac 83x \Rightarrow 8x-3y=0.$
Also, the equation of $~OB~$ is :
$~y=\frac 43 \times \frac 12x \Rightarrow 2x-3y=0.$
3. A variable straight line $~AB~$ intersecting the $~x~$ and $~y-$axes at $~A~$ and $~B~$ always passes through a fixed point $~(\alpha,\beta)~$. Find the locus of the point dividing $~AB~$ in the ratio $~2:1.$
Solution.
Let the point dividing $~AB~$ in the ratio $~2:1~$ be $~P(h,k).$
Let the equation of the straight line $~\frac xa+\frac yb=1\rightarrow(1).$
According to the problem,
$~h=\frac a3,~k=\frac{2b}{3}\\ \Rightarrow a=3h,~b=\frac{3k}{2}$
Since the straight line $~(1)~$ always passes through the point $~(\alpha,\beta)~$,
$\therefore \frac{\alpha}{a}+\frac{\beta}{b}=1 \\ \text{or,}~~ \frac{\alpha}{3h}+\frac{2\beta}{3k}=1 \\ \text{or,}~~ \frac{\alpha}{h}+\frac{2\beta}{k}=3.$
Hence, the locus of $~P~$ is $~ \frac{\alpha}{x}+\frac{2\beta}{y}=3.$
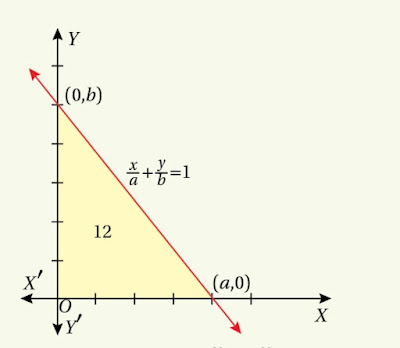
4. A straight line passes through the point $~(2,3)~$ and forms a triangle of area $~12~$ square unit with the co-ordinate axes. Find the equation of the straight line.
Solution.
The equation of the straight line in intercept form is $~\frac xa+\frac yb=1~$ where $~a=x-$intercept and $~b=y-$intercept of the line.
By question, $~~\frac 12ab=12 \rightarrow(1)~$ and the straight line passes through $~(2,3)~$, so $~\frac 2a+\frac 3b=1 \Rightarrow 2b+3a=ab.$
$\therefore~ 2b+3a=24\rightarrow(2)$
So, by $~(1)~$ and $~(2)~$ we get, $~ a=4,~b=6.$
$\therefore~$ the equation of the straight line is
$\frac x4+\frac y6=1 \Rightarrow 3x+2y=12.$
Apple 2021 10.2-inch (25.91 cm) iPad with A13 Bionic chip (Wi-Fi, 64GB) - Silver (9th Generation)
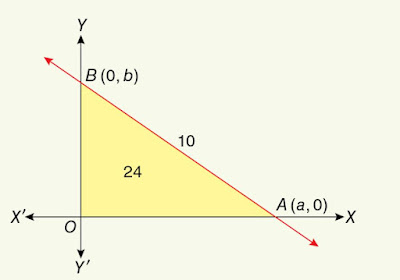
5. A straight line forms a right angled triangle with the axes of co-ordinates. If the hypotenuse is $~10~$ unit and the area of the triangle is $~24~$ square unit, find the equation of the straight line.
Solution.
The equation of the straight line in intercept form is $~\frac xa+\frac yb=1~$ where $~a=x-$intercept and $~b=y-$intercept of the line.
By question,
$~\frac 12|ab|=24 \rightarrow(1),~~\sqrt{a^2+b^2}=10 \rightarrow(2)$
Now, from $~(1),~(2)~$ we get,
$~a^2+b^2+2|ab|=100+2|ab| \\ \text{or,}~~ (a \pm b)^2=100 +2(\pm 48) \\ \text{or,}~~ (a \pm b)^2=100 \pm 96 \\ \therefore a \pm b=\pm\sqrt{100+96}=\pm 14\rightarrow(3),\\~~ a \pm b=\pm \sqrt{100-96}=\pm 2 \rightarrow(4).$
From $~(3)~$ and $~(4)~$ we get, $~~ a=\pm 8,~ b=\pm 6 ;~$ and $~a=\pm 6,~ b=\pm 8.$
So, the required equation of straight line :
$\frac{x}{\pm 8}+\frac{y}{\pm 6}=1 \Rightarrow 3x \pm 4y=\pm 24\\ \frac{x}{\pm 8}+\frac{y}{\pm 6}=1 \Rightarrow 4x \pm 3y=\pm 24.$
6. The extremities of the base of an isosceles triangle have co-ordinates $~(2a,0)~$ and $~(0,a)~$; if the equation of one of the equal sides be $~x=2a,~$ find the equations of the other two sides and the area of the triangle.
Solution.
Suppose that $~A\equiv(2a,h).$
$ \because~ AB=AC \\ \text{or,}~~ \sqrt{(2a)^2+(h-a)^2}=h^2\\ \text{or,}~~4a^2+(h-a)^2=h^2 \\ \text{or,}~~ 4a^2+h^2-2ha+a^2=h^2\\ \text{or,}~~ 5a^2-2ah=0 \\ \text{or,}~~ a(5a-2h)=0 \\ \text{or,}~~ h=\frac{5a}{2}~~[\because~ a \neq 0]$
So, the equation of $~AB~$ by joining the points $~A(2a,5a/h)~$ and $~B(0,a).$
The equation of $~AB~$ is
$~\frac{x-2a}{2a-0}=\frac{y-5a/2}{5a/2-a} \\ \text{or,}~~ \frac{x-2a}{2a}=\frac{y-5a/2}{5a/2-a} \\ \text{or,}~~ \frac{x-2a}{2a}=\frac{2y-5a}{5a-2a} \\ \text{or,}~~ \frac{x-2a}{2}=\frac{2y-5a}{3}~~(\because a \neq 0) \\ \text{or,}~~ 3(x-2a)=2(2y-5a) \\ \text{or,}~~ 3x-4y=-10a+6a \\ \text{or,}~~ 4y-3x=4a$
The equation of $~BC~$ is
$\frac{x-0}{0-2a}=\frac{y-a}{a-0} \\ \text{or,}~~ \frac{x}{-2a}=\frac{y-a}{a} \\ \text{or,}~~ x=-2(y-a) \\ \text{or,}~~ x+2y=2a$
Finally, the area of $~\Delta ABC~$ is
$=\frac 12|2a(a-0)+0+2a(5a/2-a)|\\=\frac{5a^2}{2}~~\text{sq. unit}$
7. Find the ratio in which the straight line $~5x+4y=4~$ divides the join of $~(4,5)~$ and $~(7,-1).$
Solution.
Let the ratio in which the straight line $~5x+4y=4~$ divides the join of $~(4,5)~$ and $~(7,-1)~$ be $~m:n.$
So, the co-ordinates of the point of intersection $~\left(\frac{7m+4n}{m+n},\frac{-m+5n}{m+n}\right)~$ which lies on the straight line $~5x+4y=4.~$
Hence, $~ 5 \left(\frac{7m+4n}{m+n}\right)+4\left(\frac{-m+5n}{m+n}\right)=4 \\ \text{or,}~~ 35m+20n-4m+20n=4m+4n \\ \text{or,}~~ 31m-4m=4n-40n \\ \text{or,}~~ 27m=-36n \\ \text{or,}~~ \frac mn=\frac{-36}{27} \\ \therefore~ m : n=-4:3$
8. $~A(2,5)~$ and $~B(-3,-4)~$ are two fixed points ; the point $~P~$ divides the line-segment $~\overline{AB}~$ internally in the ratio $~k:1.~$ Find the co-ordinates of $~P.~$ If $~k~$ is variable, deduce from above , the equation of the line joining $~A~$ and $~B.$
Solution.
By question, $~~P \equiv \left(\frac{-3k+2}{k+1},\frac{-4k+5}{k+1}\right).$
Since $~k~$ is variable, $\left(\frac{-3k+2}{k+1},\frac{-4k+5}{k+1}\right)=(x,y)$
$\therefore~ x=\frac{-3k+2}{k+1} \Rightarrow k=\frac{2-x}{x+3}\rightarrow(1)$
$~y=\frac{-4k+5}{k+1}\Rightarrow k=\frac{-y+5}{y+4}\rightarrow(2)$
Hence, by $~(1)~$ and $~(2)~$ we get,
$~\frac{2-x}{x+3}=\frac{5-y}{y+4} \\ \text{or,}~~ (2-x)(y+4)=(5-y)(x+3) \\ \text{or,}~~ 2y+8-xy-4x=5x+15-xy-3y \\ \text{or,}~~ 0=5x+4x-3y-2y+15-8 \\ \text{or,}~~ 9x-5y+7=0.$
Hence, the equation of the line joining $~A~$ and $~B~$ is $~9x-5y+7=0.$
9. A straight line has slope $~\frac 34~$ and it passes through the point $~A(-2,-5)~$. Find the co-ordinates of a point $~B~$ on this line where $~\overline{AB}=10~$ unit.
Solution.
The equation of line having slope $~\frac 34~$ and passing through the point $~A(-2,-5)~$ is given by :
$~y+5=\frac 34(x+2) \\ \text{or,}~ 3x-4y-14=0$
Let $~B\equiv (h,k).~$
According to the problem, $~3h-4k-14=0 \rightarrow(1)$
Again, $~\sqrt{(h+2)^2+(k+5)^2}=10 \rightarrow(2)$
From $~(1)~$ we get, $~h=\frac 13(4k+14)\rightarrow(*).$
$~h+2=\frac 13(4k+14)+2=\frac 13(4k+20)\\=\frac 43(k+5)\rightarrow(3).$
Hence, from $~(2)~$ and $~(3)~$ we get,
$~\frac{16}{9}(k+5)^2+(k+5)^2=10^2\\ \text{or,}~~ (k+5)^2 \left(\frac{16}{9}+1\right)=100\\ \text{or,}~~ (k+5)^2=100 \times \frac{9}{25} \\ \text{or,}~~ (k+5)^2=36 \\ \text{or,}~~ k+5= \pm\sqrt{36}=\pm 6 \\ \text{or,}~~ k=6-5,~-6-5 \\ \text{or,}~~ k=1,-11$
Using $~(*)~$ we get,
$~h=6,~-10~$ for respective values of $~k=1,-11.$
Explanation:
$~h=\frac 13(4 \times 1+14)=\frac 13 \times 18=6.$
$~h=\frac 13(4 \times (-11)+14)\\=\frac 13 \times (-30)=-10.$
Hence, $~B \equiv (-10,-1)~~\text{or,}~~(6,1).$





%20iPad.jpg)








Please do not enter any spam link in the comment box