Straight Line | Part-1

In the previous article, we discussed Straight Line Chapter of Ex-2A of Chhaya Mathematics, Class 11. In this article, we shall discuss about VSA type questions of Straight Line Chapter(Ex-2B).

1. The co-ordinates of the foot of the perpendicular drawn from the origin upon a line are $~(h,k)~$; show that the equation of the line is $~hx+ky=h^2+k^2~~(h^2+k^2 \neq 0).$

Solution.

If $M(x_2,y_2)$ is the foot of a perpendicular drawn from $P(x_1,y_1)$ on the line $ax+by+c=0$, then

$\frac{x_2-x_1}{a}=\frac{y_2-y_1}{b}\frac{-(ax_1+by_1+c)}{a^2+b^2}\rightarrow(1).$

By question, $~(x_2,y_2) \equiv (h,k),~~(x_1,y_1)\equiv (0,0). $

Let the equation of the line be $~y=mx+c \Rightarrow mx-y+c=0\rightarrow(2).$

So, comparing $~(2)~$ with $~ax+by+c=0~$ we get,

$~a=m,~ b=-1.$

Hence, from $~(1)~$ we get,

$~\frac{h-0}{m}=\frac{k-0}{-1}=\frac{-(m \cdot 0-1 \cdot 0+c)}{m^2+1} \\ \text{or,}~~ \frac hm=-k=\frac{-c}{m^2+1} \\ \therefore~ m=-\frac hk,\\ c=k(m^2+1)=k\left(\frac{h^2}{k^2}+1\right)=\frac{h^2+k^2}{k}$

So, $~mx-y+c=0 \\ \text{or,}~~ -\frac hk \cdot x-y+\frac{h^2+k^2}{k}=0 \\ \text{or,}~~ -hx-ky+h^2+k^2=0 \\ \text{or,}~~ hx+ky=h^2+k^2~~\text{(showed)}$

You Can Paperback

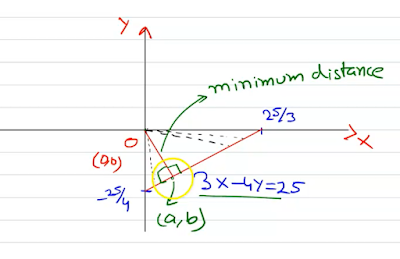
2. Find the co-ordinates of that point on the line $~3x-4y=25~$ which is nearest to the origin.

Solution.

The equation of the straight line in the intercept form can be written as

$\frac{x}{25/3}+\frac{y}{-25/4}=1$

If $M(x_2,y_2)$ is the foot of a perpendicular drawn from $P(x_1,y_1)$ on the line $mx+ny+l=0$, then

$\frac{x_2-x_1}{a}=\frac{y_2-y_1}{b}=\frac{-(mx_1+ny_1+l)}{m^2+n^2}\rightarrow(1).$

By question, $~(x_2,y_2)=(a,b),~(x_1,y_1)=(0,0),~\\~m=3,n=-4,l=-25.$

Then by $~(1)~$, we get

$\frac{a-0}{3}=\frac{b-0}{-4}=-\frac{0+0-25}{3^2+(-4)^2}\\ \text{or,}~~ \frac a3=\frac{b}{-4}=1 \\ \therefore a=3,~b=-4.$

Hence, the co-ordinates of that point on the given line which is nearest to the origin are $~(3,-4).$

3. Find the angle between the straight lines :

$(i)~~2x+3y-6=0~~\text{and}~~ 3x-2y+11=0$

Solution.

The given straight lines can be written as

$~y=(-2/3)x+2\rightarrow(1),~\\~y=\frac 32 x+\frac{11}{2}\rightarrow(2)$

The slope $(m_1)$ of $~(1)~$ is : $-\frac 23~$ and

the slope $(m_2)$ of $~(2)~$ is : $\frac 32.$

Since $~~m_1 \times m_2=-\frac 23 \times \frac 32=-1,~$ the straight lines are perpendicular to each other.

So, the angle between the given straight lines are $~90^{\circ}.$

$(ii)~~2x-y=9,~~ x-3y+8=0$

Solution.

The given straight lines can be written as

$~y=2x-9 \rightarrow(1),~~y=\frac 13 x+\frac 83\rightarrow(2).$

The slope $(m_1)$ of $~(1)~$ is : $~2~$ and

the slope $(m_2)$ of $~(2)~$ is : $\frac 13.$

If $\theta~$ be the angle between the two given straight lines then

$\tan \theta=\left|\frac{m_1-m_2}{1+m_1m_2}\right|\\ \text{or,}~~\tan\theta=\left|\frac{2-\frac 13}{1+\frac 23}\right| \\ \text{or,}~~\tan\theta=\frac{5/3}{5/3}=1 =\tan 45^{\circ} \\ \therefore \theta=45^{\circ}.$

So, the angle between the given straight lines are $~45^{\circ}.$

$(iii)~x-\sqrt{3}y=3~~\text{and}~~\sqrt{3}x-y+1=0$

Solution.

The given straight lines can be written as

$~y=2x-9 \rightarrow(1),~~y=\frac 13 x+\frac 83\rightarrow(2).$

The slope $(m_1)$ of $~(1)~$ is : $~\frac{1}{\sqrt{3}}~$ and

the slope $(m_2)$ of $~(2)~$ is : $~\sqrt{3}.$

If $\theta~$ be the angle between the two given straight lines then

$\tan \theta=\left|\frac{m_1-m_2}{1+m_1m_2}\right|\\ \text{or,}~~\tan\theta=\left|\frac{\frac{1}{\sqrt{3}}-\sqrt{3}}{1+\sqrt{3} \times\frac{1}{\sqrt{3}}}\right| \\ \text{or,}~~\tan\theta=\left|\frac{1-3}{2\sqrt{3}}\right|=\left|\frac{-2}{2\sqrt{3}}\right|\\ \text{or,}~~\tan\theta=\frac{1}{\sqrt{3}} \\ \therefore \theta=30^{\circ}.$

So, the angle between the given straight lines are $~30^{\circ}.$

Do It Today: Overcome procrastination, improve productivity and achieve more meaningful things [Paperback] Foroux, Darius Paperback

$(iv)~~y-(2+\sqrt{3})x=6~$ and $~y=(2-\sqrt{3})x+9$

Solution.

The given straight lines can be written as $~y=(2+\sqrt{3})x+6~$ and $~y=(2-\sqrt{3})x+9.$

The slope $(m_1)$ of the first straight line is : $~(2+\sqrt{3})$ and the slope $(m_2)$ of the second straight line is : $~(2-\sqrt{3}).$

If $\theta~$ be the angle between the two given straight lines then

$\tan \theta=\left|\frac{m_1-m_2}{1+m_1m_2}\right| \\ \text{or,}~~\tan\theta=\left|\frac{(2+\sqrt{3})-(2-\sqrt{3})}{1+(2+\sqrt{3})(2-\sqrt{3})}\right| \\ \text{or,}~~ \tan\theta=\frac{2\sqrt{3}}{1+2^2-(\sqrt{3})^2} \\ \text{or,}~~ \tan\theta =\sqrt{3}=\tan 60^{\circ} \\ \therefore~\theta=60^{\circ}~$

So, the angle between the given straight lines are $~60^{\circ}.$

$(v)~ax+by+c=0~$ and $~bx-ay+c_1=0$

Solution.

The given straight lines can be written as $~y=(-a/b)x-c/b~$ and $~y=(b/a)x+\frac{c_1}{a}$

The slope $(m_1)$ of the first straight line is : $~-\frac ab~~$ and the slope $(m_2)$ of the second straight line is : $~\frac ba.$

We notice that $~m_1 \times m_2=-\frac ab \times \frac ba=-1.$

So, the given straight lines are are perpendicular to each other.

Hence, the angle between the given straight lines are $~90^{\circ}.$

$(vi)~~ y=3x+5~$ and $~3y=x+7$

Solution.

The second straight lines can be written as $~y=\frac 13x+\frac 73.$

The slope $(m_1)$ of the first straight line is : $~3~~$ and the slope $(m_2)$ of the second straight line is : $~\frac 13.$

If $\theta~$ be the angle between the two given straight lines then

$\tan \theta=\left|\frac{m_1-m_2}{1+m_1m_2}\right| \\ \text{or,}~~ \tan\theta=\frac{3-\frac 13}{1+3 \times \frac 13}=\frac{8/3}{2} \\ \text{or,}~~\tan\theta=\frac 43 \\ \therefore~\theta=\tan^{-1}(4/3).$

So, the angle between the given straight lines is $~\tan^{-1}(4/3).$

$(vii)~~px-qy+r=0~$ and $~(p+q)y+(q-p)x+r=0$

Solution.

The given straight lines can be written as $~y=\frac pqx+\frac rq~$ and $~y=\frac{p-q}{p+q}~x-\frac{r}{p+q}.$

The slope $(m_1)$ of the first straight line is : $~\frac pq~~$ and the slope $(m_2)$ of the second straight line is : $~\frac{p-q}{p+q}.$

Now, $~m_1-m_2\\=\frac pq-\frac{p-q}{p+q}\\=\frac{p^2+pq-pq+q^2}{q(p+q)}\\=\frac{p^2+q^2}{q(p+q)} \rightarrow(1)$

$1+m_1m_2\\=1+\frac pq \cdot \frac{p-q}{p+q}\\=\frac{pq+q^2+p^2-pq}{q(p+q)}\\=\frac{p^2+q^2}{q(p+q)} \rightarrow(2)$

If $\theta~$ be the angle between the two given straight lines then

by $~(1)~$ and $~(2)~$ we get,

$\tan\theta=\frac{m_1-m_2}{1+m_1m_2}\\ \text{or,}~~\tan\theta=1=\tan 45^{\circ} \\ \therefore~\theta=45^{\circ}. $

Oswaal CBSE Class 11 Mathematics Question Bank (2024 Exam) Paperback

Some interesting facts about straight line :

A straight line is a one-dimensional figure that extends infinitely in both directions. It is the shortest distance between two points.

The slope of a straight line is the change in y divided by the change in x. This represents how steep the line is.
Any two distinct points on a plane can determine a unique straight line. Conversely, a line can be defined as the set of all points that satisfy an equation in two variables (typically y = mx + b).
If two lines have the same slope, they are parallel and never intersect. If two lines intersect at a right angle (90 degrees), they are perpendicular and their slopes are negative reciprocals of each other.
In geometry, a line segment is a portion of a straight line that is bounded by two distinct endpoints. A ray is a portion of a straight line that extends infinitely in one direction, while a line is a portion of a straight line that extends infinitely in both directions.
The shortest distance between two points is a straight line, also known as the distance formula. This concept is fundamental to many areas of mathematics, including calculus, geometry, and linear algebra.
A line drawn perpendicular to a straight line always passes through its midpoint. Similarly, any line that passes through the midpoint of a line segment is perpendicular to that line segment.