Differentiation (Part-38) | S N De

Straight Line | Part-6 | Ex-2A

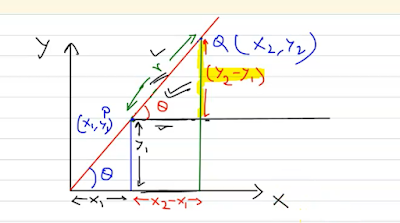
1. Define the slope of a straight line.

Solution.

The slope of a line usually gives the measure of its steepness and direction. The slope of a straight line between two points says $~(x_1,y~1)~$ and $~(x_2,y_2)~$ can be easily determined by finding the difference between the coordinates of the points. The slope is usually represented by the letter '$m$'.

If $~P(x_1,y_1)~$ and $~Q(x_2,y_2)~$ are the two points on a straight line, then the slope formula is given by: $~m=\frac{y_2-y_1}{x_2-x_1}.$

2.  State with reasons whether the equations of straight lines $~(i)~$through the origin $~(ii)~$ parallel to the $~x-$axis can be expressed in the form $~\frac xa+\frac yb=1.$

Solution.

We know that the equation of straight line in intercept form can be written as $~\frac xa+\frac yb=1~$ where $~a=x-$intercept and $~b=y-$intercept of the line.

For straight line passing through origin , $~\frac xa+\frac yb=1~$ turns out to be $~~\frac 0a+\frac 0b=0 \neq 1.$

Similarly, for the second case, the equations of straight lines parallel to the $~x-$axis can be expressed  as $~y=k~$ where $~k~$ is any arbitrary constant and so, it is evident that it can not be expressed as the form $~\frac xa+\frac yb=1.$

$3.~$ Assuming $~n~$ to be negative , express the equation of the straight line $~lx+my+n=0~$ in the normal form.

Solution.

The equation of the straight line $~lx+my+n=0~$ in the normal form can be written as 

$~\frac{l}{\sqrt{l^2+m^2}}~x+\frac{m}{\sqrt{l^2+m^2}}~y=-\frac{n}{\sqrt{l^2+m^2}}.~~(n <0)$

4.  The straight line joining the points $~P(x_1,y_1)~$ and $~Q(x_2,y_2)~$ makes an angle $~\theta~$ with the positive direction of $~x-$axis; prove that, $~x_2=x_1+r\cos\theta~$ and $~y_2=y_1+r\sin\theta~$ where $~r=\overline{PQ}.$

Solution.

According to the problem and from the picture, 

$~\frac{x_2-x_1}{r}=\cos\theta \Rightarrow x_2=x_1+r\cos\theta,\\~\frac{y_2-y_1}{r}=\sin\theta \Rightarrow y_2=y_1+r\sin\theta.$

5.  Find the area of the triangle formed by the straight line $~x\cos\alpha+y\sin\alpha=p~$ with the axes of co-ordinates.

Solution.

Let $~O~$ be the origin and the line meets $~x-$ axis and $~y-$axis at $~D~$ and $~E~$ respectively. 

For $x-$axis $~y=0~$ and so,

$~ x\cos\alpha+0=p\Rightarrow x=p\sec\alpha.$

Hence, $~OD=p\sec\alpha.$

Similarly, for $y-$axis $~x=0~$ and so,

$~0+y\sin\alpha=p\Rightarrow y=p\csc\alpha$

Hence, $~OE=p\csc\alpha.$

So, the area of the triangle formed by the given straight line is

$=\frac 12 \times OD \times OE\\=\frac 12 \times p\sec\alpha \times p\csc\alpha\\= p^2 \cdot \frac{1}{2\sin\alpha\cos\alpha}\\=\frac{p^2}{\sin2\alpha}\\=p^2\csc2\alpha~~\text{sq. unit.}$

6.  The point $~P~$ divides the line-segment joining the points $~A(x_1,y_1)~$ and $~B(x_2,y_2)~$ in the ratio of $~m:n.$ If $~P~$ lies on the line $~ax+by+c=0~,$ prove that,

$~\frac{m}{n}=-\frac{ax_1+by_1+c}{ax_2+by_2+c}$ 

Solution.

By question, co-ordinates of $~P\equiv\left(\frac{mx_2+nx_1}{m+n},\frac{my_2+ny_1}{m+n}\right)$

Now, since $~P~$ lies on the line $~ax+by+c=0~,$ so

$~a\left(\frac{mx_2+nx_1}{m+n}\right)+b\left(\frac{my_2+ny_1}{m+n}\right)+c=0 \\ \text{or,}~~ amx_2+anx_1+bmy_2+bny_1+c(m+n)=0 \\ \text{or,}~~ m(ax_2+by_2+c)+n(ax_1+by_1+c)=0 \\ \text{or,}~~ \frac{m}{n}=-\frac{ax_1+by_1+c}{ax_2+by_2+c}$

Physics Galaxy 2020-21: Electrostatics & Current Electricity - Vol. 3A Paperback

7.  Show that the equation of the straight line joining the points $~(a,b)~$ and $~(c,d)~$ can be written as $~(x-a)(y-d)=(x-c)(y-b).$

Solution.

Let $~P(x,y)~$ be any point on the straight line joining the points $~(a,b)~$ and $~(c,d)~$ . Now, we know that the slope $(m)$ of a straight line is same everywhere and so,

$~m=\tan\theta=\frac{\text{change in ordinate}}{\text{change in ordinate}} \\ \text{or,}~~\frac{y-b}{x-a}=\frac{y-d}{x-c} \\ \text{or,}~~ (x-a)(y-d)=(x-c)(y-b).$