Differentiation (Part-38) | S N De

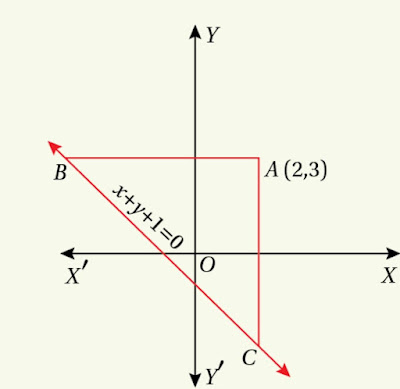
18.  The equation of the hypotenuse of an isosceles right angled triangle is $~x+y+1=0~$and the co-ordinates of its opposite vertex are $~(2,3)~$. Find the equations of the other two sides of the triangle.  

Solution.

The equation of any sl passing through the point $~(2,3)~$ and having slope $~m~$ can be written as 

$~y-3=m(x-2) \rightarrow(1)$

Since the triangle is an isosceles right angled triangle, so

$~\tan 45^{\circ}=\left|\frac{1+m}{1-m}\right| \\ \text{or,}~~ \frac{1+m}{1-m}=\pm 1 \\ \text{or,}~~ 1+m=\pm(1-m) \\ \therefore~ m=0~~\text{and}~~ m=\infty.$

For $~m=0,~$ we get by $~(1)~,~~ y-3=0.$ 

For $~m=\infty,~$ we get by $~(1)~,~~ x-2=0.$ 

Hence,  the equations of the other two sides of the triangle are $~x-2=0,~~y-3=0.$

19.  The co-ordinates of the ends of one diagonal of a rectangle are $~(6,1)~$ and $~(12,9).~$ If its other diagonal be parallel to the $~x-$axis, then find the co-ordinates of its ends.

Solution.

Since its other diagonal be parallel to the $~x-$axis, the co-ordinates of the ends of this diagonal are $~(x_1,b)~$ and $~(x_2,b)~~\text{(say).}$

Clearly, $~\frac 12(x_1+x_2)=\frac 12(12+6) \Rightarrow x_1+x_2=18.$

Also, $~b=\frac{9+1}{2}=5.$

Again, $~\text{slope of}~AB \times \text{slope of }~BC=-1 \\ \therefore~ \frac{b-9}{x_1-12} \times \frac{b-1}{x_1-6}=-1 \\ \text{or,}~~ \frac{5-9}{x_1-12} \times \frac{5-1}{x_1-6}=-1 \\ \text{or,}~~ \frac{-4}{x_1-12} \times \frac{4}{x_1-6}=-1 \\ \text{or,}~~ (x_1-12)(x_1-6)=16 \\ \text{or,}~~x_1^2-18x_1+72-16=0 \\ \text{or,}~~ x_1^2-18x_1+56=0 \\ \therefore (x_1-4)(x_1-14)=0 \\ \text{or,}~~ x_1=4,14.$

For $~ x_1=14,~~x_2=4~~$ and for $~ x_1=4,~~x_2=14.$

Hence, the co-ordinates of  the ends of the diagonal are $~(4,5)~$ and $~(14,5).$

20.  Show that the four lines $~y=0,~y=2,~y-\sqrt{3}x=0~$ and $~y+\sqrt{3}x=8\sqrt{3}~$ form a cyclic trapezium. Find the co-ordinates of its vertices and also its area.

Solution.

Given four lines are $~OA \equiv y=0 \rightarrow(1),~ BC \equiv y=2\rightarrow(2) ,~ OC\equiv y-\sqrt{3}x=0 \rightarrow(3)~$ and $~AB \equiv y+\sqrt{3}x=8\sqrt{3} \rightarrow(4)~$. 

Solving respective equations , we get 

$~O \equiv (0,0),~A \equiv(8,0),~B\equiv \left(8-\frac{2}{\sqrt{3}},~2\right),C \equiv \left(\frac{2}{\sqrt{3}},2\right).$

Since the quadrilateral $~OABC~$ has two parallel sides , so $~OABC~$ forms a trapezium.

Now, the slope of $~OC~=\sqrt{3},~$ the slope of $~BC~=-\sqrt{3}.$

$ \therefore~ \angle{AOC}+\angle{ABC}=\angle{AOC}+\angle{BAX}=180^{\circ}$

So, $~OABC~$ is a cyclic trapezium.

Now, $~OA=8~$ unit and $~BC=8-\frac{4}{\sqrt{3}}.$ 

$ \therefore~$ Area

$=\frac 12 \left(8+8-\frac{4}{\sqrt{3}}\right) \times 2~~[*]\\=4\left(4-\frac{1}{\sqrt{3}}\right)~~\text{sq. unit.}$

Note :$[*]~~ \text{Area}=\frac 12(OA+BC) \times h.$

21.  Prove that the diagonals of the parallelogram formed by the lines $~\frac xa+\frac yb=1,~\frac xb+\frac yb=1,~\frac xa+\frac yb=2~$ and $~\frac xb+\frac ya=2~$ are at right angles to each other.

Solution.

Let $~AB \equiv \frac xa+\frac yb=1,\\~BC\equiv \frac xb+\frac ya=1,\\~DC \equiv \frac xa+\frac yb=2,\\~AD \equiv \frac xb+\frac ya=2. $

Now, the perpendicular distance between $~AD~$ and $~BC~$

$d_1=\left|\frac{1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}}\right|$

and the perpendicular distance between $~AB~$ and $~DC~$

$d_2=\left|\frac{1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}}\right|$

$ \because~ d_1=d_2~,$ so the parallelogram $~ABCD~$ is a rhombus.

So, its diagonals bisect each other at right angles and hence follows the result.

22.  The sides $~AB,~BC,~CD~$ and $~DA~$ of a quadrilateral have the equations $~x+2y=3,~x=1,x-3y=4~$ and $~5x+y+12=0~$ respectively. Find the angle between the diagonals $~AC~$ and $~BD.$

Solution.

We have, $~AB \equiv x+2y=3 \rightarrow(1),\\~BC \equiv x=1 \rightarrow(2),\\~CD \equiv x-3y=4 \rightarrow(3),\\~ DA \equiv 5x+y+12=0 \rightarrow(4).$

Solving $~(1),~(4)~$ we get, $~ A\equiv (-3,3).$

Solving $~(1),~(2)~$ we get, $~ B\equiv (1,1).$

Solving $~(2),~(3)~$ we get, $~ C\equiv (1,-1).$

Solving $~(3),~(4)~$ we get, $~ D\equiv (-2,-2).$

Now, the slope of $~AC~$ is $~(m_1)=\frac{-1-3}{1+3}=-1~$ and the slope of $~BD~$ is $~(m_2)=\frac{-2-1}{-2-1}=1.$

$ \therefore~ m_1 \times m_2=-1 \times 1=-1.$

$~\therefore~ $ the angle between the diagonals $~AC~$ and $~BD~$ ia $~90^{\circ}.$